Examples
FizzBuzz
The FizzBuzz problem is extremely contrived yet popular so we will start with it as it is our simplest example. The problem is to print the numbers 1 to 100 on new lines, but if the number is divisible by 3 print "Fizz" and/or if divisible by 5 print "Buzz", and do not print the number if it is divisible by either.
Mainstream languages my find it shorter to handle the 3, 5 cases separately, but since it is so easy to loop in iogii we will handle these in a loop. So here is some pseudocode for what we will implement:
map 1 to 100 as i:
a = zip 3,5 and "Fizz","Buzz" as j and k:
k if i divides j else ""
concat(a) or str(i)
This pseudocode returns a list of strings. Iogii implicitly prints values and a list will print newlines after each element.
We won't need explicit loops thanks to vectorization. We can set i with:
100 countTo let i →
This didn't print anything since let sets the variable and eats it.
This next loop looks more complicated, but let's just set j and k similarly. Where j and k are actually used is where we will need to make sure it is the correct "type of loop". We can control if they are being used like a nested loop or a zip by how we shape the data.
3,5 let j "Fizz","Buzz" let k →
There is no divides op in iogii, but it can be achieved by checking if the remainder is 0. In these examples I'll actually set i to be 1 to 15 instead of 100 just to keep the output size reasonable. If we wanted to get all the remainders of i and 3 we could just do so by:
15 countTo 3 % → [1,2,0,1,2,0,1,2,0,1,2,0,1,2,0]
But if we want to get the remainders of 3 and 5 this won't work:
15 countTo 3,5 % → [1,2]
Because doing a scalar operation on two vectors (rank 1 lists) just does a zip. Doing it on a vector and scalar also did a zip but it broadcasted the scalar to a list first, but a vector doesn't needed to be implicitly broadcasted first.
However we can do what we want by manually broadcasting the 3,5 ourselves:
3,5R
3 5
3 5
3 5
3 5...
Note that single line examples with a → show the value pretty printed (what the show op does). But examples with a horizontal line show what iogii actually will print, which I did here to show the shape better.
R just did a once unvectorized repeat. If we had used an r it would have generated the transpose of that value.
Now when we do this:
15 countTo 3,5R%
1 1
2 2
0 3
1 4
2 0
0 1
1 2
2 3
0 4
1 0
2 1
0 2
1 3
2 4
0 0
We get what we want and it is actually the 1 to 15 that must broadcast to reach a high enough rank (but broadcasting maximally vectorizes implicitly so we didn't need to proceed it with an r).
Ok now we can just take the not on each value (since only 0 is falsey) to find if the number is divisible or not.
15 countTo 3,5R%n
0 0
0 0
1 0
0 0
0 1
1 0
0 0
0 0
1 0
0 1
0 0
1 0
0 0
0 0
1 1
Ok now to use this as the condition to our if statement, I'll go back to using variables too. The ifElse op takes condition, true result, and false result as args. We need to unvectorize it once, because even though the condition is maximally vectorized we want to return a string (which is a list of characters). (You specify the most unvectorized arg for ops with two type variables).
15 countTo let i
3,5 let j
"Fizz","Buzz" let k
i j R %n k "" IfElse
Fizz
Buzz
This didn't work. Why? Because it didn't know to vectorize the condition and broadcast the "Fizz" and "Buzz". It just said: is first list element empty? then "Fizz" and is second element empty? then "Buzz" and the first list element is indeed not empty (it is [0,0]).
We can just repeat the FizzBuzz however, because now it knows it is doing a vectorized op since there is excess rank for that arg, and it will prefer to vectorize into the other arg since it has a different type variable. We use R, (twice unvectorized) since "Fizz","Buzz" is a rank two list and we want to repeat the entire thing to match the shape.
15 countTo let i
3,5 let j
"Fizz","Buzz" let k
i j R %n k R, "" IfElse show
[["",""],["",""],["Fizz",""],["",""],["","Buzz"],["Fizz",""],["",""],["",""],["Fizz",""],["","Buzz"],["",""],["Fizz",""],["",""],["",""],["Fizz","Buzz"]]
Now the final thing to do is concat each of these sublists and use i str if empty, which we can do with an ifElse again.
15 countTo let i
3,5 let j
"Fizz","Buzz" let k
i j R %n k R, "" IfElse concat dup i str IfElse
1
2
Fizz
4
Buzz
Fizz
7
8
Fizz
Buzz
11
Fizz
13
14
FizzBuzz
We used dup since if truthy we want to use that same value as the true value too.
Ok so we have a working solution, now let's golf it.
j and k are only used once, so let's just inline those.
15 countTo let i
i 3,5 R %n "Fizz","Buzz" R, "" IfElse concat dup i str IfElse
1
2
Fizz
4
Buzz
Fizz
7
8
Fizz
Buzz
11
Fizz
13
14
FizzBuzz
Also let's replace all ops with their one character name at this point and remove all spaces:
15} let i
i3,5R%n"Fizz","Buzz"R,""Yu:i`Y
1
2
Fizz
4
Buzz
Fizz
7
8
Fizz
Buzz
11
Fizz
13
14
FizzBuzz
The str op is unneeded since ints will automatically coerce to a string since both true and false values have the same type variable. We can also remove this ifElse altogether by using a max on our concatenated string and our integer (since the string value of the integer is greater than the empty string). This op will also coerce and it must also be capitalized since we are returning a string (rank 1) for each value.
15} let i
i3,5R%n"Fizz","Buzz"R,""YuiX
1
2
Fizz
4
Buzz
Fizz
7
8
Fizz
Buzz
11
Fizz
13
14
FizzBuzz
Now let's return to looking at the other ifElse. One idea is to just use string replication * to replicate a string 0 or 1 times instead. That would be:
15} let i
"Fizz","Buzz"R,i3,5R%n*uiX
1
2
Fizz
4
Buzz
Fizz
7
8
Fizz
Buzz
11
Fizz
13
14
FizzBuzz
Now let's get rid of the let statement. The value i is used twice and not near each other in the syntax tree so no duplicate op can help use. Since there is no input to the this program and only one value is used twice we are guaranteed to be able to use set implicit value for the other use - which would be optimal, but let's look at using a duplication op as a matter of taste.
The first use of i has three ops applied to it before it is used again, so mdup can't be used. But the max op is commutative so we could swap its arg order.
15} let i
i"Fizz","Buzz"R,i3,5R%n*uX
Now i is left intact before it is used again, but there's an extra item on the stack. This is what the peek op is for, so let's use it:
15} let i
i"Fizz","Buzz"R,]3,5R%n*uX
Now i is used only once so we can inline it:
15}"Fizz","Buzz"R,]3,5R%n*uX
1
2
Fizz
4
Buzz
Fizz
7
8
Fizz
Buzz
11
Fizz
13
14
FizzBuzz
Finally let's try to improve "Fizz","Buzz"R,. We could replace "Fizz","Buzz" with "FizzBuzz" 4 reshape, but we can do even better because we want the result repeated which cost us an extra comma for the R, so if we repeat before we reshape we can do that with just an R since that rank is lower than after the reshape:
15}"FizzBuzz"R4#]3,5R%n*uX
1
2
Fizz
4
Buzz
Fizz
7
8
Fizz
Buzz
11
Fizz
13
14
FizzBuzz
It's also worth noting that we could use 2 pow10 (2H) instead of 100. This gives us a completed FizzBuzz in 26 characters and none of them built specifically for this problem... I thought this was optimal, but while writing this example tutorial I actually found a way to save another character. I don't want to spoil the problem however, can you find it too?
Pi
Pi is a classic code golf problem. Let's print pi, with the decimal point, to 100 decimal places.
Iogii doesn't have BigDecimal or even floating point numbers so we will need to represent it using a large integer instead, we can just calculate pi * 10^100 using integers. There are numerous algorithms for pi, but typically spigot algorithms are the best because they don't have to deal with rounding errors messing us up (for other algorithms we might need to calculate more than 100 digits and then truncate which takes more code).
Here is the spigot algorithm we are interested in:
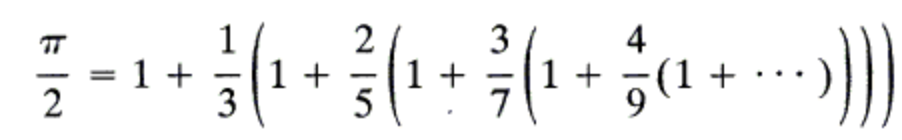
Our method for doing math will be standard for languages with big integer built in. We will keep our result as 10^100 (2HH) times that result, so when adding a regular number to this number we must multiply by 2HH first. We can multiply by fractions as is. If we wish to multiply our result by itself we would need to divide by 2HH afterwards, etc. (fortunately we don't need to do other types of operations here).
Let's write out a few terms manually then generalize it:
2HH 5* 11/ 2HH+ 4* 9/ 2HH+ 3* 7/ 2HH+ 2* 5/ 2HH+ 1* 3/ 2HH+ 2*
31215007215007215007215007215007215007215007215007215007215007215007215007215007215007215007215007214
So we start with 0, then add 2HH, then multiply by the numerator and divide by the denominator. We could do this with an iterate.
0 iterate 2HH+ 5,4,3,2,1* 11,9,7,5,3/ > 2*
0
9090909090909090909090909090909090909090909090909090909090909090909090909090909090909090909090909090
12929292929292929292929292929292929292929292929292929292929292929292929292929292929292929292929292928
14112554112554112554112554112554112554112554112554112554112554112554112554112554112554112554112554112
13645021645021645021645021645021645021645021645021645021645021645021645021645021645021645021645021644
11215007215007215007215007215007215007215007215007215007215007215007215007215007215007215007215007214
We only want the last value, so we will do that, but we actually need to add 2HH to that final value so let's move that 2HH+ to the end of the loop and add an extra term so we still get the same result:
0 iterate 6,5,4,3,2,1* 13,11,9,7,5,3/ 2HH+ > last 2*
31215007215007215007215007215007215007215007215007215007215007215007215007215007215007215007215007214
Now we could generate those descending sequences with things like countTo reverse but this problem begs to be solved with a foldr instead of an interate since we only want the final result. Since foldr also works right to left, any list that is being used with the intermediate results also needs to be reversed (which will actually be easier since the lists are descending).
0 foldr 1,2,3,4,5,6* 3,5,7,9,11,13/ 2HH+ > 2*
31215007215007215007215007215007215007215007215007215007215007215007215007215007215007215007215007214
A 0 foldr is just a meld. And we can just generate these sequences more easily now:
meld 6 countTo* 6 countTo 2* succ / 2HH+ > 2*
31215007215007215007215007215007215007215007215007215007215007215007215007215007215007215007215007214
Let's replace things by their one character name at this point and experiment to find how many iterations we need to converge:
m 333 }* 333 } 2* ) / 2HH+ > 2*
31415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170678
That last digit should be a 9 actually, luckily? if we put the 2* inside the iteration instead of being done at the end the value is not rounded too low.
m 333 }* 333 } 2* ) / 2HH2*+ >
31415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679
This is already looking very concise, but here are some ideas:
- Don't rewrite
333} - Arrange things so that
>can be implicit. - Possibly use
:+instead of2*. - Use
3Hinstead of 333 (can't hurt to do more iterations). - Realize that one of those integer sequences could actually be infinite, the other finite one will cause it to truncate when we do an op with it.
- Finish the problem by printing the decimal point somehow.
- If there is a way to generate pi - 3 then that could be very useful.
- Consider doing 10,000 iterations that way we could dup and take the square root to also get the value 100 (not directly shorter but maybe could be useful).
- Consider other order of operatios to possibly use a sequence starting at 1 that counts by 2 (instead of starting at 3).
Let's do 4. and remove spaces (since the others are possibly all related).
m3H}*3H}2*)/2HH2*+>
31415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679
We also should consider that we could swap the order things are done so that the second sequence could go down to 1 instead of 3 (I don't think that works in this case though).
If we use the :+ trick on 3H} then we are actually using it 3 times, seems like a good candidate for setting it to be the implicit value. But to take full advantage of that we would have to structure it to something like:
3H} code1 3H} code2 3H} > code3
Where code1 doesn't use the 3H}, the second 3H} will be $ implicitly placed with rotation trick, and the third 3H} will be present followed by > to set the implicit values.
Unfortunately we can't make the denominator be in the beginning because it is the second arg to /. So that would mean code2 is no op and 2nd+3rd uses make the denominator. But this won't work because we can't use implicit values until we consume everything on the left but the loop var from meld will need to be to the left of the denominator.
So our next best is to just use normal stack manipulation to duplicate the 3H}. We use it after a single op, so we can use mdup again.
m3H};*2*)/2HH2*+>
31415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679
We can't omit the > because the loop could have terminated after the `/'. We need to arrange things so that the stack size never is 1. And we have many options since there are 3 places we can duplicate values.
Some arrangements calculate the wrong digit for the first digit, which may not matter depending on how to print the decimal point, so let's look at that first. One idea is to convert it to a string, tail it, then print the rest:
"3." 12345 `t
3.2345
Or
3'.12345`t
3.2345
However there is a better way, which is to do a string join with ".","","","","" .... And fortunately we can generate that succinctly with:
'.Z → [".","","",...
This works because '. rank is too low, so it promotes to ".", then Z zero pads (default value for rank 1 is empty list/string).
String join uses subsequent values from the second arg if there is more than one for each insertion. Also string join is special in that it will promote each character to a string if you use it on a rank 1 list, since it needs a rank 2 list but making a large single element list would be useless. We can also give it an int so long as one arg is a string and it will coerce.
314159'.Z* → "3.14159"
So this is 1 character shorter than the truncation method. Meaning if we rearrange things to save a character for > and don't calculate the first digit correctly then we won't save anything.
We haven't explored all our ideas yet, but let's stop here and put all together, we get:
m3H};*2*)/2HH2*+>'.Z*
3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679
Which solves this problem in 21 characters. Like FizzBuzz it is possible to save at least another character (my best is 20) but I don't want to completely spoil the challenge.
More examples coming soon!
Debugging
Debugging a lazy functional program can be tricky. show can be used to pretty print values before the rest of the output.
Getting folds/iterates correct can also be tricky due to their circular/infinite nature. I recommend first writing the code that maps desired input to desired output for the function of the fold, and then calling it manually with all examples at once (so that you are using it vectorized like the real function will be).
For example, for the fibonacci program. Let's we could say our inputs are 1 1 2 3 we can just test those rather than the infinite list:
1,1,2,3 set inputs inputs 0 cons + → [1,2,3,5]
And that is our desired output since 1 iterate will prepend the 1 for us.