iogii
Iogii is an esoteric programming language, designed to be concise yet simple, making it fun to use in code golf. It is built around a technique known as circular programming, which is actually useful for real-world functional programming.
Iogii uses postfix notation (e.g. 3 2 1+* → 9) which removes the need for parenthesis. To do looping operations like iteration and folding, other postfix languages require stack manipulation to place function args in the correct locations (which is both tedious and verbose). But thanks to a novel use of circular programming, iogii never needs to manipulate the stack.
Instead iogii does these looping operations by placing a regular value on the stack, they can be placed exactly where you need them because they are unconstrained by special syntax. Additionally, this lets iogii double down on being good at manipulating values - doing so makes it better at manipulating loops too!
See also: Why
Example
This program generates the Fibonacci numbers and then keeps the first 10:
1 iterate dup 0 cons + 10 keep → [1,1,2,3,5,8,13,21,34,55]
This is parsed like any other expression, iterate acts like a regular unary op on its initial value of 1. dup duplicates the top of the stack. cons prepends an element to a list. It could also have been written:
1i:0c+10k → [1,1,2,3,5,8,13,21,34,55]
This page will give you enough of an overview of the language to understand this example. If you want to golf competitively in it, the docs will teach you everything else there is to know about it.
Just remember, simple does not mean easy.
Overview
Syntax
All ops have both verbose name(s) and a one character name. In this tutorial, I am using the long form for clarity.
Expression syntax is postfix. Every operation pops the necessary number of arguments, computes the result and pushes it. Even things like numbers (they are just functions of 0 arguments). Be sure to read up on this if it is new to you.
5 2 1+* → 15
Here is the stack after each token in this program:
5 : 5
2 : 5 2
1 : 5 2 1
+ : 5 3
* : 15
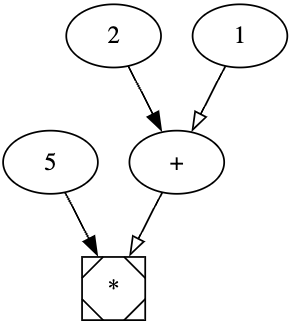
Although technically Iogii doesn't actually push and pop values from a stack, it is a static language so it constructs a tree/graph that is later turned into values. 5 2 1+* encodes this tree:
An exception to postfix is the data format, which is numbers, chars, or strings, separated by commas:
1,2,3 → [1,2,3]
"asdf","1234" → ["asdf","1234"]
You may use two or more ,s to separate between higher ranks:
1,2,,3,4 → [[1,2],[3,4]]
Strings are just a list of characters
'a,'b,'c → "abc"
For more information about syntax, see the syntax doc.
Vectorization
All operations vectorize (similar to APL or numpy).
1,2,3 4,5,6+ → [5,7,9]
With broadcasting as needed:
1,2,3 2+ → [3,4,5]
Even ops that take arbitrary types:
"abc","123" head → "a1"
head gets the first element from a list, so it would have returned "abc" except that it vectorized and got the first element of "abc" and "123" which were 'a and '1 respectively.
If we wish for these generic ops to not vectorize, capitalize them or proceed them with a ,. This is why generic ops use alphanumeric names instead of symbols.
"abc","123" Head → "abc"
Similarly to zipWith in Haskell, lists of different lengths are truncated when doing a vectorized operation:
"abcde" 1,2,3 + → "bdf"
For more information about vectorization, see the vectorization doc.
Laziness
The language is functionally pure and lazy. This is useful for working with infinite lists:
wholes 5 keep → [0,1,2,3,4]
wholes is the infinite list of whole numbers. keep is an op that keeps the second arg number of elements from the first. In short form this would have been:
{5k → [0,1,2,3,4]
Laziness is also useful for avoiding special syntax for conditionals. For example, you can write an if statement as so:
[condition] [trueCase] [falseCase] ifElse
E.g.
0 3 3+ 1 1+ ifElse → 2
Thanks to laziness we don't need special syntax and the trueCase is only evaluated if the condition is truthy and the falseCase is only evaluated if falsey. Here computing 3+3 would not be expensive, but this could be invaluable for infinite lists or expressions that would error.
Looping
In functional programming, the most common types of looping (or recursion) are:
- Map (applying a unary function to a list)
- Zips (applying a binary function to two lists)
- Iterate (applying a unary function repeatedly)
- Folds (applying a binary function to reduce a list to a single value)
- Scans (folding but accumulating intermediate values)
Map and zip are accomplished via vectorization. Folds, scans, and iterate are accomplished via looping operators. This set of operations is very powerful, even an O(n log n) merge sort can be written with just them (although something like quicksort would be difficult due to the irregular sizes in the recursive step).
In this overview we will look at iterate, but the other looping operations are similar.
Functions
iterate acts like a value, but it also needs to allow you to express a function. To do this iterate stands in place of the function arg and also gets passed the result of a matching end bracket (>). For example:
0 iterate 1+ > → [0,1,2,3,...
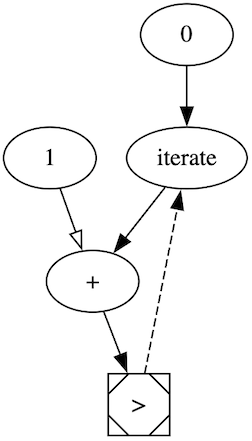
This is like giving the function (λx.x+1) to the iterate op.
iterate didn't have to be the first thing in that function, for example, we could represent (λx.1-x) like so:
1 0 iterate - > → [0,1,0,1,0...
iterate really does act like a regular value to make this happen.
You may have noticed that our original Fibonacci numbers example did not use the end bracket (>). If end brackets are missing, they are implicitly inserted at the first valid location. A function can only return one value so our first iterate example here could not have terminated after the 1, therefore the > could have been omitted (same with our other example). See > matching for more information about bracket matching.
Circular Programming
In Haskell, iterate starts with some value and then applies some function to that value and then again to that result and so on. But in iogii the function is applied to all previous values in one call to the function using vectorization. In fact, [initial] iterate [function] > is actually just syntactic sugar for result [function] [initial] cons set result (where set binds the result of the previous value, cons, to the next identifier, result). The final intermediate representation graph that iogii generates has no concept of functions at all, only values.
Our counting iterate example generates this graph:
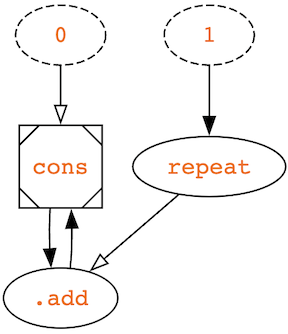
Which is the same graph you would get from this code:
result 1+ 0 cons set result → [0,1,2,3,4...
This may seem paradoxical, how can we pass in all inputs to the function when all but the first of those inputs are the result of that same function? Remember that iogii is a lazy language. Defining a function in terms of itself (recursion) is well understood, this is defining a value in terms of itself (co-recursion), which is not as familiar since it would be nonsensical in a non-lazy language.
If you take the head (first element) of this, it is 0, you don't need to look beyond the first argument to cons to calculate that, so lazy languages don't.
What is the head of the tail, i.e. the second element? Well, the first arg to cons is the tail and that is: result 1+. Since + is a vectorized operation, the first element of this is just 1 plus the head of result (and we already know the result head is 0), so the answer is 1. And so on and so forth. As long as we construct our circular programs in a way that no value depends on itself or infinite other values, it will terminate.
Circular programming is not something specially coded into iogii, it is a natural consequence of laziness and these techniques can be used in languages like Haskell too. You can learn more about it in the circular programming part of the docs.
This may still seem strange. Why do it like this?
Because it allows for all sorts of concepts to be unified.
Let's look at what would happen if instead of adding 1, we add a list:
0 iterate 4,5,6+ → [0,4,9,15]
It performed a scanl! (which is just a left fold but capturing the value at each step). Since the yielded value was a list, this + operation just did a vectorized + with that list and 4,5,6. At each step, it is adding the next number to the sum-so-far resulting in the next sum-so-far. This time the result is not an infinite list, because vectorization truncates to the shorter of its operands.
So using the same op, iterate, we can iterate but also perform a scanl. There are many other possibilities, these ops work with just values so you can use them in any way you want with any op and any structure.
Also, notice that our scanl was tacit, there are no identifiers to describe args, nor was any stack manipulation necessary. Many languages can do that for trivial cases like this, but break down for more complicated expressions.
Back to our example, this is similar to how our Fibonacci example worked:
1 iterate dup 0 cons + → [1,1,2,3,5,...
It is doing a vectorized add of two lists, the loop var and a 0 consed loop var. Prepending to the list offsets it so that each result is the sum of a number and the previous number.
Next steps
Hopefully, this overview was educational for you even if you have no intention of ever using iogii. You can play around and test things out with the online interpreter (which also creates the diagrams used on this page).
If you want to get started golfing in iogii, try some problems from: code.golf, golf.shinh.org, or codegolf.stackexchange.com.
The quickref and docs will be your friend.
There's also a discord server, feel free to join!
I built iogii to be the language I wished existed for code golf. It is simple yet has the features I love: tacit, lazy, vectorized, one letter/symbol per op, no syntactic cruft. Which is why, i only golf in iogii.